Single Value Tree

November 30th, 2017

Another popular tree question:

Given a binary tree, count the number of unival subtrees(all nodes having the same value). For e.g. in the tree below, all the subtrees enclosed in ellipses are unival trees.

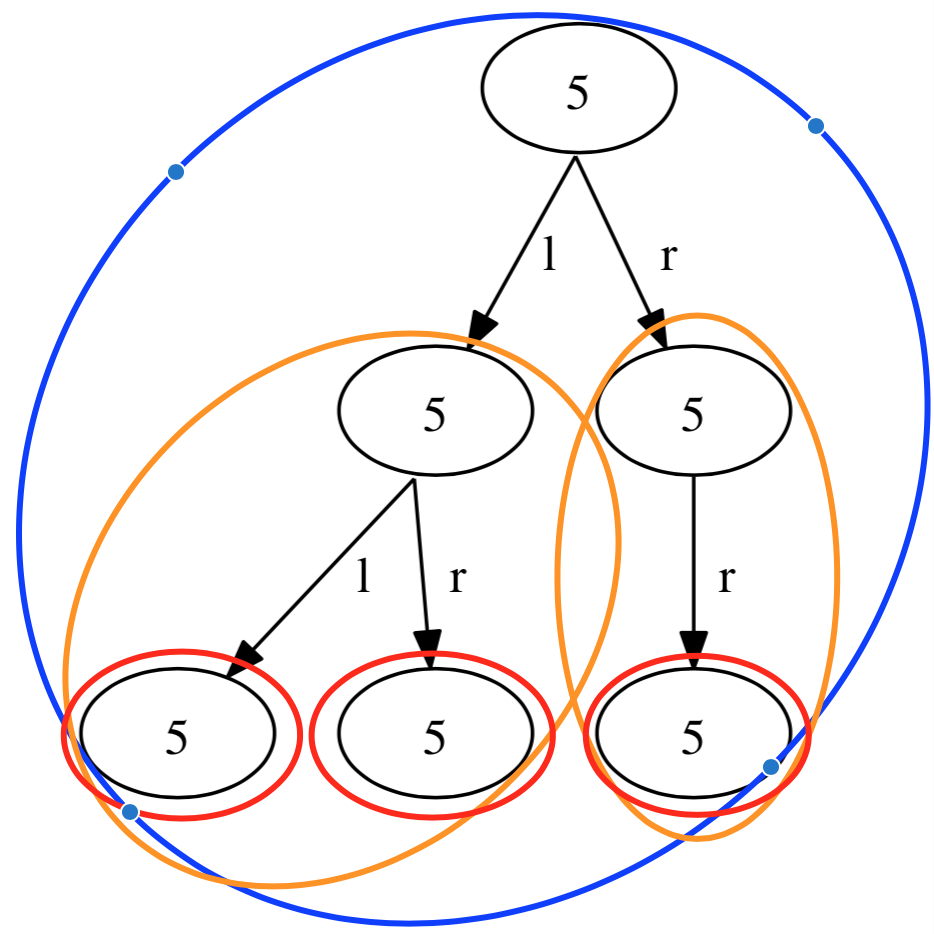
unival_tree

Above tree was generated using the graphviz library. The result for the tree above would be 6. There is a C++ implementation around. The time complexity is O(n).

The ruby implementation looks a lot simpler owing to the fact that it can return multiple values. Here it is:

# let's quickly create a tree
class Node < Struct.new(:val, :left, :right); end
root = Node.new(5)
root.left = Node.new(5)
root.left.left = Node.new(5)
root.left.right = Node.new(5)
root.right = Node.new(5)
root.right.right = Node.new(5)

# this function returns true if:
# a. child is nil
# b. child is not nil and it has same value as parent plus it's subtree is a unival until the child
def is_unival?(node, child, is_child_unival)
  is_child_unival && (child.nil? || node.val == child.val)
end

def unival_subtrees(node)
  # if node is nil, the subtree count is obviously 0 and it is unival
  return [true, 0] if node.nil?
  is_left_unival, left_count = unival_subtrees(node.left)
  is_right_unival, right_count = unival_subtrees(node.right)
  # check is left and right subtrees are unival and the current node and children have same values
  if is_unival?(node, node.left, is_left_unival) &&
     is_unival?(node, node.right, is_right_unival)
    # Add one more subtree which includes current node to the total count
    [true, left_count + right_count + 1]
  else
    [false, left_count + right_count]
  end
end

# test by calling the unival_subtrees method
unival_subtrees(root)
=> [true, 6]

This was a fun question to solve. Let me know your thoughts in comments. Cheers!!!